算法基础 | FLY

插入排序

伪代码

伪代码是有代码规则的

INSERTION-SORT(A)
for i=2 to A.length
    key = A[i]
    //将A[i] 插入到 A[1, ..., i-1]
    j = i - 1
    while j>0 and A[i] > key
        A[j+1] = A[i]
        j = j - 1
    A[j+1] = key

循环不等式

其实就是 $A[1, …, i-1]$ 序列中不变的性质，在上述插入算法中的循环不等式的性质就是序列是递增序列；

循环不等式的，必须证明三条性质：

1. 初始化：循环的第一次迭代之前，它为真；
2. 保持：如果循环的某次迭代之前它为真，那么下次迭代之前它仍为真；
3. 终止：在循环终止时，不变式为我们提供一个有用的性质，该性质有助于证明算法是正确的

伪代码一些约定

缩进表示块结构；
for while repeat-until等循环结构以及if－else等条件结构与其他语言有类似的结构；其中to表示递增，downto表示递减，还有当循环计数器以大于1的一个量改变时，该改变量更在可选关键词by之后，其实就是每次循环的改变量，即step步数
//表示注释
i=j=e表示多重赋值，即i=e, j=e；
无显示说明，不使用全局变量；
通过下标访问数组元素；
NIL表示空；布尔运算符都是短路运算即只有为true之后的运算就掠过；
所有为值传递；

分析算法

分析一个算法的优劣，会有很多的影响因素比如内存、硬件资源、网络资源等，还包括数据类型、内存模型、计算机指令等因素；

输入规模量度，用来表示输入规模，比如输入是一个图，则输入规模可以用定点个数和边数来进行描述；

以上述的插入排序进行分析

最优情况

即输入序列是正序；

最差情况

输入序列是倒序，这个比较看重，因为这是一个算法的上限，而且它出现的概率比较大比如检索时找不到；

平均情况

往往与最差情况差不多

增长量级

进一步的抽象，将常系数和低阶项抽象；

设计算法

上述的插入排序使用的增量法，即将单个元素插入到适当位置

分治法

思想

将原问题分解为几个规模较小但类似于原问题的子问题，递归地求解这些子问题，然后在合并这些子问题的解来建立原问题的解；
步骤
1. 分解，分解原问题为多个小问题；
2. 解决，解决小问题；
3. 合并，合并小问题的解为原问题的解；
实例，归并排序
适用
1. 该问题的规模缩小到一定的程度就可以容易地解决；
  
  绝大多数问题都可以满足的，因为问题的计算复杂性一般是随着问题规模的增加而增加
2. 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质
  
  是应用分治法的前提它也是大多数问题可以满足的，此特征反映了递归思想的应用
3. 利用该问题分解出的子问题的解可以合并为该问题的解；
  
  关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法
4. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题
  
  涉及到分治法的效率，如果各子问题是不独立的则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然可用分治法，但一般用动态规划法较好

分析分治算法

递归式分析

分治算法运行时间的递归式来自基本模式的三个步骤：假设T(n)是规模为n的一个问题的运行时间,

若问题的规模足够小，比如某个常量 $c$ （即规模为 $c$ 的问题），当 $c \le n$ 时，则可以直接求解，也就是说规模 $c$ 是一个界值，这时可以将其时间复杂度写作 $O(1)$ ；
否则，把原问题分解成 $a$ 个子问题，每个子问题的规模时原问题的 $1/b$ （ $a$ 不一定就 $==b$ ，在二分归并排序时时相等的）；为了求解一个规模为 $n/b$ 的子问题，需要 $T(n/b)$ 的时间，所以需要 $aT(n/b)$ 的时间来求解 $a$ 个子问题
若分解成子问题需要时间 $D(n)$ ，合并子问题的解成原问题的解需要时间 $C(n)$ ;

递归式为：

T(n) = \begin{cases} \Theta(1), & \text{if } n \le c \\ aT(n/b)+D(n)+C(n), & \text{other} \end{cases}

这是针对一个问题的一个层级进行分析的；其实也是利用递归

归并排序算法的分析

分析结果是其运行时间为 $O(n\lg n)$ ；

分析建立归并排序n个数的最坏运行时间 $T(n)$ ，

当 $n＝1$ 时即归并一个元素需要一个常量时间（即在排除其他影响下，该时间是一个常量）;

当 $n>1$ 时，分析如下：

分析：分析步骤仅计算子数组的中间位置，这里也是一个常量时间，即 $D(n) = O(1)$ ；

解决：递归的求解两个规模均为 $n/2$ 的子问题，将贡献 $2T(n/2)$ 的运行时间；

合并：在一个具有 $n$ 个元素的子数组上进行merge需要 $O(n)$ 的时间，所以 $C(n)=O(n)$ ；

由上图并结合2.2的讲解，即当 $n>1$ 时， $T(n) = 2T(n/2)+O(1)+O(n)$ ，因为 $F(n)=O(n)+O(1)$ 是一个 $n$ 得一个线性函数，所以可得

T(n) = \begin{cases} \Theta(1), & \text{if n=1} \\ 2T(n/2)+\Theta(n), & \text{if n>1} \end{cases}

假设常量c代表求解规模为1得问题所需得时间以及在分解步骤与合并步骤处理每个数组元素所需得时间；则可以将递归式图2.1重写为

T(n) = \begin{cases} c, & \text{if n=1} \\ 2T(n/2)+cn, & \text{if n>1} \end{cases}

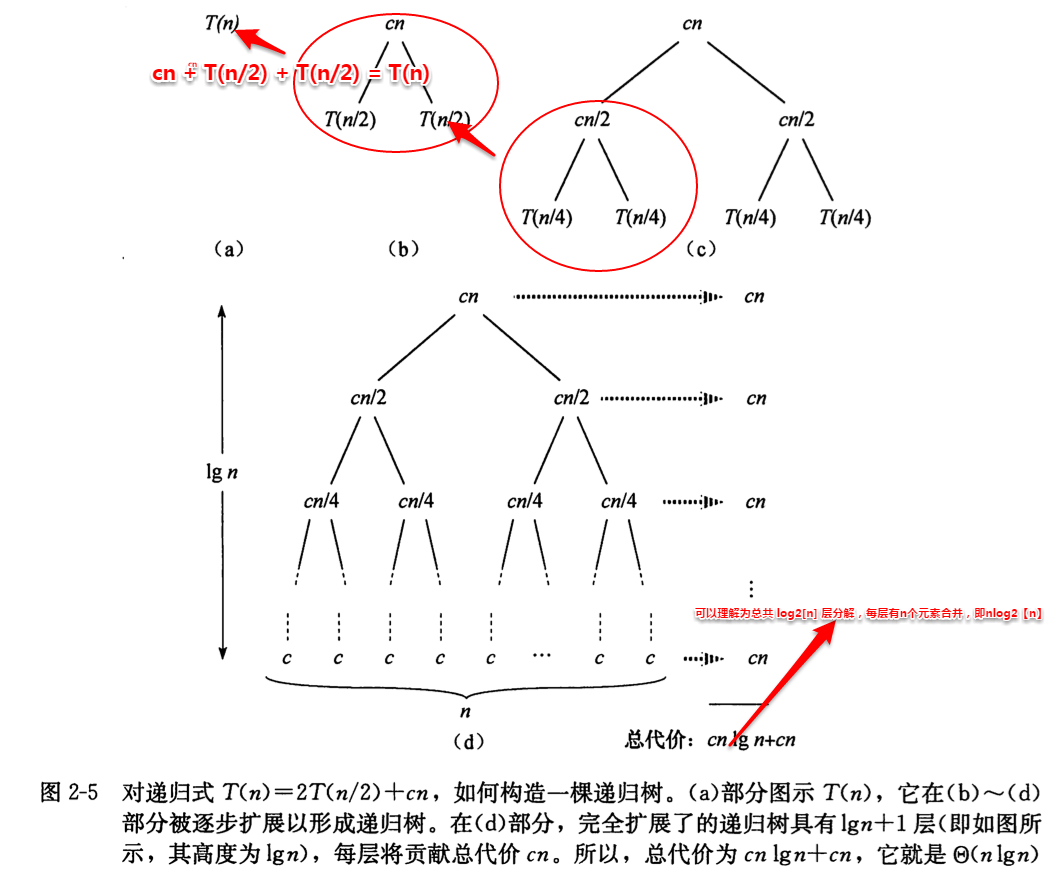
注意看分析，其实T(n) = Θ(合并每层的时间) x 总行数 = $nlog_2^n$