[TOC]
渐进符号
渐进确界
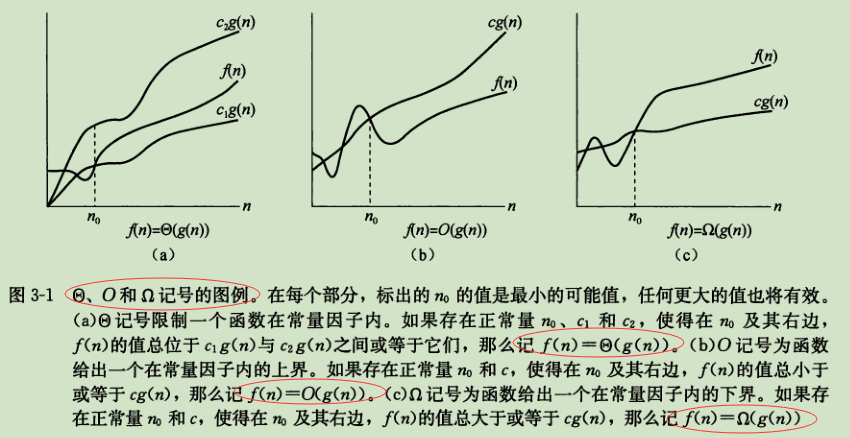
Θ
- 表示一个函数的上限与下限,可以理解为f(n)是集合Θ(n)中的一个函数;
Θ(g(n)) = {f(n):存在正常量c1,c2和n0,使得对于所有的n≥n0,有0≤c1∗g(n)≤f(n)≤c2∗g(n)}

渐进上界
O
表示一个函数的上限,O(g(n)) = {f(n):存在正常量c和n0,使得对所有n≥n0,有0≤f(n)≤cg(n)
渐进下界
Ω
表示一个函数的下限, Ω(g(n)) = {f(n):存在正常量c和n0,使得对所有n≥n0 ,有0≤cg(n)≤f(n);
定理
对任意两个函数f(n)和g(n),我们有f(n)=Θ(g(n)),当且仅当f(n)=O(g(n))且f(n)=Ω(g(n))
等式和不等式的渐进符号
当渐进符号出现在等式中时,它一般代表某个我们不关注的匿名函数,这样可以帮助消除一个等式中无关紧要的细节与混乱;比如2n2+3n+1=2n2+θ(n),θ(n)表示某个函数f(n),该函数是集合θ(n)的某个函数;可以使用以下规则来解释:无论怎样选择等号左边的匿名函数,总有一种办法来选择等号右边的匿名函数使等式成立;换句话说,等式右边比左边提供的细节更粗糙。
非渐进紧确的上界
o
o(g(n)) = {f(n):对于任一正常量c>0,存在常量n0>0,使得对所有n≥n0,有0≤f(n)<cg(n),即
n→+∞limg(n)f(n)=0
非渐进紧确的下界
ω
定义的一种方式:f(n)∈ω(g(n)),当且仅当g(n)∈ο(f(n));
ω(g(n)) = {f(n):对于任一正常量c>0,存在常量n0>0,使得对所有n≥n0,有0≤cg(n)< f(n)},即
n→+∞limg(n)f(n)=∞
函数性质

三分性
对于任意两个实数a,b,下列三种情况恰有一种必须成立:a>b,a=b,a<b;但两个函数f(n)和g(n),不是都可以渐进比较的;
标准记号与常规函数


